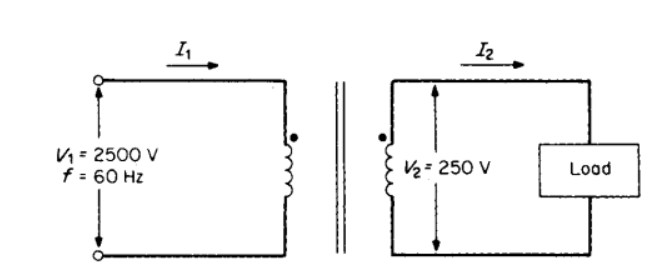
To compute the number of primary and secondary turns:
\[ N_1 = \frac{V_1}{\text{Voltage per Turn}} \]
\[ N_2 = \frac{V_2}{\text{Voltage per Turn}} \]
To compute the full-load currents:
\[ I_1 = \frac{\text{VA}}{V_1} \]
\[ I_2 = \frac{\text{VA}}{V_2} \]
Let's assume the following values:
Step 1: Compute the number of primary and secondary turns:
\[ N_1 = \frac{2500}{2.5} = 1000 \text{ turns} \]
\[ N_2 = \frac{250}{2.5} = 100 \text{ turns} \]
Step 2: Compute the full-load currents:
\[ I_1 = \frac{25000}{2500} = 10 \text{ A} \]
\[ I_2 = \frac{25000}{250} = 100 \text{ A} \]