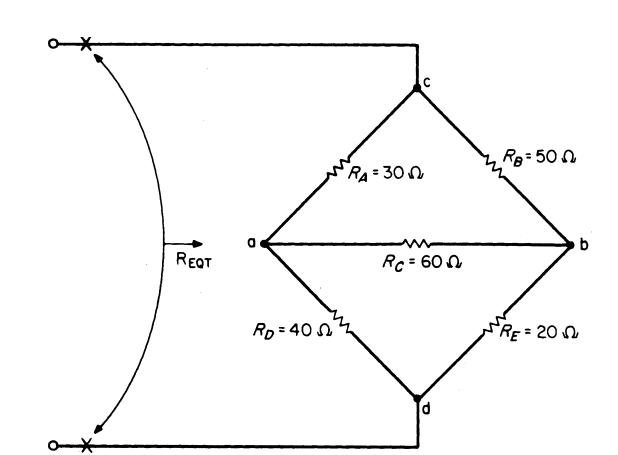
The formulas for wye-delta transformation are:
\[ R_1 = \frac{R_A \cdot R_C}{R_A + R_B + R_C} \]
\[ R_2 = \frac{R_B \cdot R_C}{R_A + R_B + R_C} \]
\[ R_3 = \frac{R_A \cdot R_B}{R_A + R_B + R_C} \]
Let's assume the following values:
Step 1: Apply the wye-delta transformation formulas:
\[ R_1 = \frac{R_A \cdot R_C}{R_A + R_B + R_C} = \frac{30 \cdot 60}{30 + 50 + 60} = 12.9 \text{ Ω} \]
\[ R_2 = \frac{R_B \cdot R_C}{R_A + R_B + R_C} = \frac{50 \cdot 60}{30 + 50 + 60} = 21.4 \text{ Ω} \]
\[ R_3 = \frac{R_A \cdot R_B}{R_A + R_B + R_C} = \frac{30 \cdot 50}{30 + 50 + 60} = 10.7 \text{ Ω} \]
Step 2: Calculate the equivalent resistance \( R_{EQ} \):
\[ R_{EQ} = R_1 + \left(\frac{R_2 \cdot R_D}{R_2 + R_D}\right) = 12.9 + \left(\frac{21.4 \cdot 40}{21.4 + 40}\right) = 33.9 \text{ Ω} \]